Profile of a perfect application – Maths
Over the next year we’ll be publishing a series of articles explaining how you can put together a perfect application for Oxford or Cambridge in various subjects. As applications increase in difficulty, there is an ever-more important drive towards perfection – anything less than this might see a really good candidate just fall short of the necessary standard. By reading this series you’ll understand what it takes and, hopefully, put it into motion yourself!
Maths
Mathematics is the cornerstone of so many science and social science subjects that it is sometimes hard to remember that is a subject in its own right. The reality is that Maths is not only a fantastic subject, it’s probably the best way to guarantee a job at any top firm in the world. Numerical analysis is vitally important in research, private and governmental sector roles. Be wary though, it’s very different from the maths you study at GCSE or A Level. The theory is more complex and may be less applicable to real world situations that you’re probably familiar with.
Before applying make sure you check out some learning modules online that give you an example of how universities teach this subject. The best place to find this is through an online MOOC. Here’s a link to some good examples.
https://www.my-mooc.com/en/categorie/mathematics
https://www.coursera.org/courses?query=mathematics
https://www.mooc-list.com/tags/math
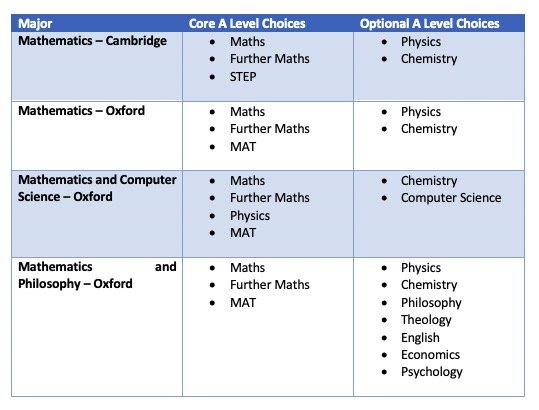
Grades and Subject Choices
The right subject choices depend on which your final choice of major, but getting the right selection is vital. Here are some of our top tips:
Projects
There are a vast array of potential projects that Economics applicants can choose from. Whether it’s using words or numbers, the key is to plenty and win prizes. You’ll need at least 10 different projects and activities to be considered by Oxbridge. Here is an example of a good prize to enter if you’re aiming for perfection:
Maths Olympiad
The International Mathematical Olympiad (IMO) is the World Championship Mathematics Competition for High School students and is held annually in a different country. The first IMO was held in 1959 in Romania, with 7 countries participating. It has gradually expanded to over 100 countries from 5 continents. The IMO Board ensures that the competition takes place each year and that each host country observes the regulations and traditions of the IMO. Sample questions are below.
Check out our website for more!
Admissions Tests
Applicants are going to be set entry tests for any of these courses. At Oxford, around 40% of candidates are interviewed and the decision in invite or reject a student is based largely on the PS, your grades and these entry tests. The score you get is essential for winning a place. Only around 5 – 10% of applicants get a conditional offer. Score above 70% and you’ll be taking your first step on the highways towards getting an offer. If you score less than 67% your chances are low, and less than 65% will make getting an offer impossible. You must aim for 70% as a minimum and a ‘perfect applicant’ will get 72% or more. The margins are small!
Interviews
By far and away the most interesting part of the interview process, a perfect applicant is expected to have the right approach to answering questions, and manage to obtain the correct answer in 60% of the scenarios with little or no assistance. A further 20% should be accessible with some coaching from the interviewer whilst the very best candidates will be able to access all answers with some guidance.
For Maths at Cambridge, candidates can expect 5 or 6 questions that are predominantly numbers-based. You should be able to get the answers for all 5 with coaching.
Question 1)
There's a torus/ring doughnut shaped space station with 2 spacemen on a spacewalk standing diametrically opposite each other. Can then ask a variety of questions such as if spaceman A wants to throw a spanner to spaceman B, what angle and speed should they choose (stating any assumptions made, e.g. that gravity = 0)?
Question 2)
Show that if n is an integer, n^3 - n is divisible by 6.
Contact us today for answers to these questions or for answers to your own questions. We’re always happy to help with any element we can.